FishTest est l’environnement de test des nouvelles versions de StockFish.
C’est un environnement distribué de non régression. Réalisé en langage Python par Gary Linscott, c’est la première fois qu’un moteur de jeu d’Echecs est testé intensivement dans un environnement multi-OS (Windows et Linux), multi-PC, multi-cores CPUs et surtout multi-testeurs.
L’aventure de FishTest est très récente puisqu’elle a débuté en avril 2013. Elle relance le développement de SF car avoir des idées d’améliorations du moteur c’est bien mais prouver leurs efficacité sans entraîner de non régression, là est la vraie difficulté de la programmation échiquéenne de haut niveau.
Un environnement distribué de test pour SF
Le 1er mai 2013, Marco Costalba publie Fishtest Distributed Testing Framework dans TalkChess une introduction sur FishTest créé par Gary Linscott. L’annonce est d’autant plus importante qu’elle justifie le saut dans les versions de SF de 2.x à 3.0.
L’idée est de distribuer l’effort de test sur plusieurs machines dont les propriétaires acceptent de donner du temps CPU. Qui est concerné ? Tout le monde ayant un PC sous Windows ou Linux avec au moins 4 CPUs (QUADS) dont un à 3 core CPUs prêtés pour FishTest via Internet. Inutile de postuler avec un portable duo-core qui n’est pas fait pour tourner en continue avec un seul core CPU dédié au test de SF car les moteurs d’échecs font chauffés les machines surtout en été. Il faut donc un PC costaud avec un gros ventilateur qui fonctionne parfaitement. Certains gamers utilisent même des systèmes externes de refroidissement.
Télécharger FishTest librement depuis son espace Git.
On trouvera les commandes à lancer après enregistrement permettant d’avoir son login.
Langage : Python 2.7.4 (framework Pyramid Application Development)
Chess GUI : cutechess-cli (C++ avec framework Qt) permet l’automatisation des duels de moteurs d’échecs paramétrés en ligne de commande.
Gary Linscott reprend dans clop_worker le principe de CLOP (Confident Local Optimization for noisy black-box Parameter tuning) de Rémi Coulom avec certaines différences présentées par Marco Costalba.
Base de données sur le serveur : MongoDB énorme (humongous) base de données en C++ non SQL.
Tout est transparent pour le testeur qui reçoit automatiquement les exécutables à tester ou à compiler, les jeux de tests. Le script Python renvoie les résultats au serveur agrégés par Google Groups dans FishCooking Results.
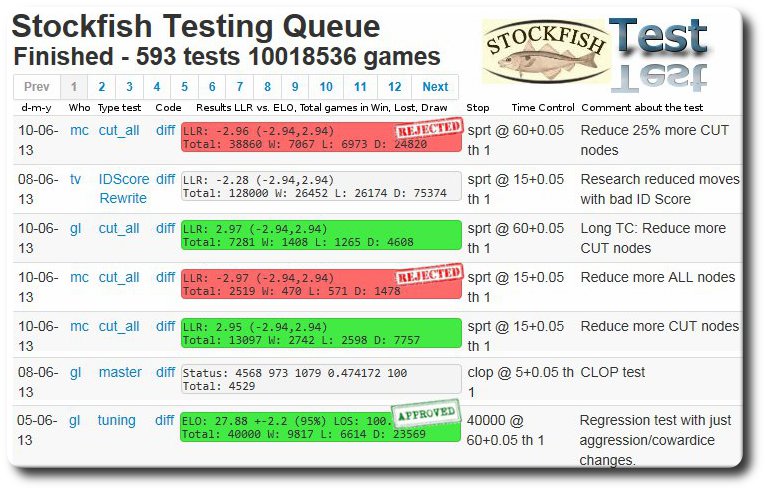
Les résultats sont automatiquement compilés sur le site SF Testing Framework : SF testing queue.
Les chiffres parlent d’eux-mêmes : 16 machines, 68 cores CPU, 1.31 M node per second en million, 30 games par minute.
Patch approuvé
En vert sont les patches qui ont réussi la campagne de test. Ils gagnent le droit de passer à l’étape suivante 60+0.05 (long TC = Time Control), la 1ère étape étant avec le contrôle de temps 15+0.05 (short TC).
Exemple : 4/6/13 testeur gl, type de test : tuning, diff, "Regression test with all successful weight tests"
ELO : 27.32 +-3.7 (95%) LOS : 100.0% Total : 13621 W : 3331 L : 2262 D : 8028
Estimation du gain en Bayesian ELO de Rémy Coulom, un compétiteur d’EloStat de Frank Schubert. Le Bayesian ELO est généralement supérieur à l’ELO réel.
Il y a 95% de chance que le vrai ELO soit dans l’intervalle [27.32-3.7, 27.32+3.7]=[23.62,31,02]
LOS (Likelihood Of Superiority) est le pourcentage statistique de certitude de l’hypothèse H0 le patch est meilleur que la référence par rapport à H1 il y a une régression. Ne pas confondre LOS avec lost.
Total indique le nombre de parties de jeux d’échecs jouées réparties en Win, Lost, Draw.
Patch rejeté
En rouge sont les patches qui ont échoué et sont abandonnés. Ils sont plus nombreux que les verts. Cela veut dire que l’équipe SF ne fera par un COMMIT dans Git du patch dans la branche principale (master) de SF.
Certains patches verts et tous les patches rouges présentent l’abréviation LLR. C’est le Log Likelihood Ratio, un critère statistique d’arrêt des tests quand on atteint ou sort de la fenêtre (lower_bound upper_bound).
Pour évaluer les différentes approches, on distingue deux types d’erreurs et la moyenne d’arrêt
- Erreur de Type I : faux positif. Un mauvais patch est accepté à tort. Comportement risqué. Type1 elo loss signifie combien d’ELO est perdu à cause des patches à ELO négatif acceptés à tort.
- Erreur de Type II : faux non positive. Un bon patch est rejeté à tort. Comportement conservatif. Type2 elo loss signifie combien d’ELO est perdu à cause de patches à ELO positif refusés à tort.
- Avg(stop) : combien de tests doit on exécuter en moyenne avant de terminer la campagne.
Efficacité de la campagne selon critère de stop
La récompense ou efficacité se traduit en terme de jeux de tests que l’on a évité et qui statistiquement ne devrait pas changer le résultat quant à l’acceptation ou le refus du patch. On parle également de meilleure précision car à effort de test constant, on utilise mieux les ressources CPU distribuées en réseau sur les patches qui sont les plus prometteurs en terme d’ELO.
Deux écoles pour le critère d’arrêt des tests s’affrontent :
- Méthode discrète d’arrêt au plus tôt des tests. On sait à l’avance le nombre de tests à faire réparti selon la règle des trois tiers. T = 16000 games. Le domaine d’application est la non régression. De combien la nouvelle version a progressé en ELO ?
- Méthode SPRT (Sequential Probability Ratio Test) Le domaine d’application est la validation de patch. Le patch est-il pire ou meilleur que la référence ? On ne cherche pas à savoir de combien il est meilleur ou pire en valeur absolue.
Autoréglage de la fonction d’évaluation
Joona Kiiski a publié Stockfish’s Tuning Method dans Chess Programming une méthode originale d’autoréglage de la fonction d’évaluation de SF. L’idée est d’organiser un duel self-play entre deux versions de SF l’une étant réglée avec la borne min du paramètre à régler et l’autre avec la borne max, le +/- delta étant environ à 20% de la valeur actuelle de la version de référence. L’environnement de non régression FishTest est alors utilisé pour tester massivement les deux versions.
Dans le cas d’un gain manifeste du match, on fait évoluer tout doucement la valeur du paramètre dans le sens du vainqueur selon delta / 500. Le processus converge s’il y a un seul paramètre clef à régler. Cependant le problème est complexe dans le cas de plusieurs paramètres à régler ensemble (on parle alors de vecteur de paramètres). Vu macroscopiquement, cela s’apparente à une variante de la méthode dichotomique avec un delta et une progression de la valeur du paramètre à régler qui sont particulièrement plus faibles nécessitant beaucoup de duels et donc de temps CPU.
On pourra approfondir le sujet avec les remarques de Robert Hyatt (Crafty), Rémi Coulom (CLOP), Marco Costalba (StockFish).